Objective
A key step to accomplish the green energy transition is to develop and deploy environmentally, economically, and sustainable alternatives to fossil fuel energy production. Proven technologies to produce electrical power from sustainable sources like the wind, the sun, and the sea are widely available. However, if the amount of produced electrical power exceeds the actual need at a given moment, means are needed to store the surplus for later use. Power-to-X (PtX) conversion technologies can transform electrical power into other forms of energy (typically heat) or a wide array of chemicals (hydrogen, ammonia, methanol, methane, synthetic fuels, etc.), which can be efficiently stored for later use.
While various PtX technologies exist and have proved to be viable in large-scale power plants, a lot of work is still being done on improving their economic viability and efficiency. One such technology is the electrolyzer, which uses electricity to separate water into hydrogen and oxygen. Hydrogen can be stored and used, for example, to generate electricity using a fuel cell at a later time or to produce climate-neutral synthetic fuels.
Resolvent has developed alkaline electrolyzer cell models which can be used to support the optimization of different cell designs and operating conditions, see Figure 1 for a description of a generic alkaline electrolyze cell.
In this first part of this series of posts, we will address how the models are set up and highlight what kind of results can be obtained from such models. In an upcoming post, we will discuss how we can use such models to optimize the design and operating conditions of the cells.

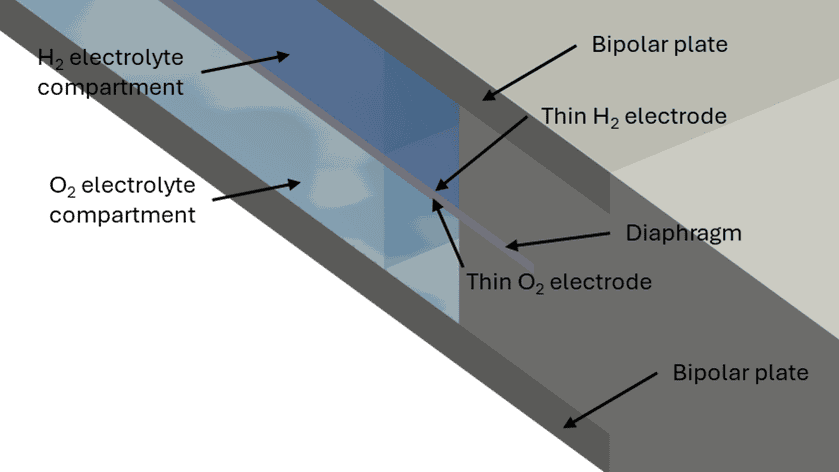
Figure 1: Alkaline electrolyzer cell, (a) Full cell geometry with cut plane at the center of the cell and (b) zoom in on the cross-section of the cell showing individual components
Challenge
In an alkaline electrolyzer cell, different physical phenomena occur at different scales and interact with each other. This results in a highly non-linear and strongly coupled system of equations that must be solved simultaneously.
A liquid electrolyte, typically a mixture of water and potassium hydroxide (KOH) is pumped through each half-cell. By applying an electric current to the cell, water is split into hydrogen and oxygen gas at the cathode and anode, respectively. The gas bubbles are dragged by the liquid electrolyte and buoyancy forces upwards (y-direction in Figure 1) where they are collected and leave the cell.
How much gas is produced locally across the surface of each electrode depends on, among other things, operating conditions (pressure, temperature, applied current) and local cell resistance. During operation, the liquid and gas mixture is heated up from the inlet (bottom) to the outlet (top) of the cell, which affects the equilibrium potential of the half-cell reactions. In general, higher temperatures offer better electrochemical performance, which should result in an increased current density at the top of the cell. However, other competing phenomena, such as the amount of gas bubbles present at the electrodes blocking reaction sites, can increase cell resistance locally. This can be more pronounced at the top of the cell where the gas accumulates before leaving the cell. At a given total current, the overall current density distribution across the active area of the cell will thus be a result of the balance between the competing processes mentioned above and other inefficiencies in the system.
To predict the cell performance with enough precision to optimize its design, those processes must be accounted for in the simulation model. From a computational fluid dynamics point of view, a multiphase flow model needs to be adopted to prescribe the flow properties of the liquid electrolyte and gaseous hydrogen or oxygen bubbles. Depending on the size of the cell and the location in the cell (manifold or electrolyte compartment), the flow regime can either be laminar or turbulent. The gas phase source terms are determined by the electrochemical reaction rates, which in turn depend on the availability of electrolyte and local current density. All the above are directly or indirectly affected by the temperature, which can either be prescribed in the model (e.g., isothermal assumption or prescribed temperature profile) or solved by the model.
Combining all these phenomena results in a multiphase, multiphysics simulation model.
Solution
Modelling Approach
Before setting up an optimization strategy for the alkaline electrolyzer cell’s geometry and operating conditions, a simulation model was developed in COMSOL Multiphysics © including all relevant physics. The following main modelling assumptions were made:
- A temperature profile is prescribed varying linearly from 70°C to 80°C from the inlet to the outlet of the cell
- Hydrogen and oxygen crossover through the diaphragm is neglected
- The electrodes, located on each side of the diaphragm (zero-gap cell), are modelled as thin electrodes
- Fluid properties are evaluated at operating pressure and local temperature, except for density, which is evaluated at operating pressure and temperature (constant)
- Electrode kinetics and half-cell reaction equilibrium potentials are temperature dependent
- The diameter of the gas bubbles is constant
- Only hydrogen and oxygen are present in the gas bubbles (dry gas)
- Stack level losses are not considered (e.g., shunt currents through the stack manifolds)
Some of the above simplifications were made to decrease model complexity and lower computational time. It was deemed that they would not affect the optimization parameters of interest significantly and thus were reasonable assumptions.
For instance, a linear temperature profile was prescribed from the lowest to the highest part of the active area, which is a first step towards relaxing the isothermal approximation. The model thus captures temperature dependent effects without having to solve for the temperature field explicitly. The next step would be to add an additional equation for the conservation of energy and solve for the temperature field.
Studies
The initial approach was to solve all relevant physics (multiphase flow, current conservation, etc.) in a stationary study. However, due to the geometry of the cell manifold and the dynamics of the eddies generated by the small “jets” at the bottom of the cell, the equations were instead solved in a time-dependent study, where the electrolyte flow rate and total cell current were progressively ramped up.
Results
For a given set of operating conditions (operating temperature, pressure, electrolyte flow rate, electrolyte concentration, and applied current) the model calculates the following fields at all points within the electrolyte compartments, cell manifolds, diaphragm, and/or across active area of each half-cell:
- Liquid electrolyte velocity, pressure, and volume fraction
- H2 and O2 gas velocity, pressure, and volume fraction
- H2 and O2 reaction rates
- Electric current and potential
- Electrolyte current and potential
From those, it is possible to calculate secondary variables of interests which will be used in the optimization phase, e.g., flow rates through each cell manifold channel, statistics on the residence time of the liquid electrolyte and gas bubbles in the cell, etc.



Figure 2: Example of output from the multiphase, multiphysics model of an alkaline electrolyzer cell, (a) Mixture velocity magnitude, (b) dispersed phase (gas) volume fraction, and (c) current density distribution at the electrodes
Benefits for our customers
The simulation models of a single cell developed by resolvent offer a platform which can be used to perform sensitivity studies and optimize the operating conditions and geometrical dimensions of the cell. Being able to virtually test how geometrical changes and various operational conditions impact the performance of the alkaline electrolyzer cell offers a great advantage for our customers, who can investigate many design iterations quickly, without having to build costly prototypes and run costly and time-consuming physical tests. The models can thus be used to accelerate the development of such critical technologies that are required for a successful green energy transition. More on this will be covered in the next part of this blog post series.
Software and areas of expertise used
- COMSOL Multiphysics®
- Multiphase computational fluid dynamics
- Turbulent flow
- Electrochemistry
Knowledge and opportunities generated
The multiphysics models developed offer a valuable understanding on how relevant quantities such as velocity, gas, and liquid volume fractions, pressure, flow distribution across the cell manifold, current distribution, etc., change with operating conditions and for a given geometry. Those models serve as a solid foundation for the optimization of the cell design.
Stay tuned to hear about how resolvent used the models, set up their optimization strategy, and what kind of performance indicators were analyzed in an upcoming post.
Industry
Power to X